Tutorial
Linear Vs Binary Search via JavaScript

While we believe that this content benefits our community, we have not yet thoroughly reviewed it. If you have any suggestions for improvements, please let us know by clicking the “report an issue“ button at the bottom of the tutorial.
JavaScript comes with some pretty handy out-of-the-box tools for searching through an array. But with a large data set the O(n) methods like indexOf, find, or a basic loop just aren’t the best or even feasible. Instead, we can use Binary search to go over an array without looking at what we obviously don’t need, giving us a O(logn) solution.
Prerequisites
I will be using Big O Notation when comparing performance and complexity, which you can brush up on here.
Practice Data
Here are some sorted and unsorted datasets, both with 50 items, that I’ll be referencing.
const unsortedArr = [31, 27, 28, 42, 13, 8, 11, 30, 17, 41, 15, 43, 1, 36, 9, 16, 20, 35, 48, 37, 7, 26, 34, 21, 22, 6, 29, 32, 49, 10, 12, 19, 24, 38, 5, 14, 44, 40, 3, 50, 46, 25, 18, 33, 47, 4, 45, 39, 23, 2];
const sortedArr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50];
Linear Search
This is the standard brute-force solution I’m sure you’ve already done a thousand times. We’re just telling it, “I need something, so look through everything one-by-one until you find it”. If there’s a million times more items, it’ll take a million times longer, which nobody is going to put up with. Whether the data is sorted or not makes no difference.
const linear = (arr, target) => {
let steps = 0;
for (let i = 0; i < arr.length; i++) {
steps++;
if (arr[i] === target) return `Found: ${arr[i]} in ${steps} steps`;
};
};
console.log(linear(unsortedArr, 40)); // 40 steps in 40 Milliseconds
console.log(linear(sortedArr, 40)); // 40 steps in 40 Milliseconds
Binary Search
Brute-forcing your way to a result is obviously a very slow and unscalable solution. Instead of wasting resources looking at data that’s obviously not what we want, we can use a ‘divide-and-conquer’ approach to make each operation focus on ignoring what we don’t want instead of painfully looking for what we do want.
We have three main components, two pointers and one pivot. Each pointer starts at the either end of the array with the pivot in the center. Then we check if what we want is higher or lower than our pivot, if higher then the left pointer is moved to the pivot’s position while the pivot moved to the new middle. We keep running this until our pivot is equal to our target.
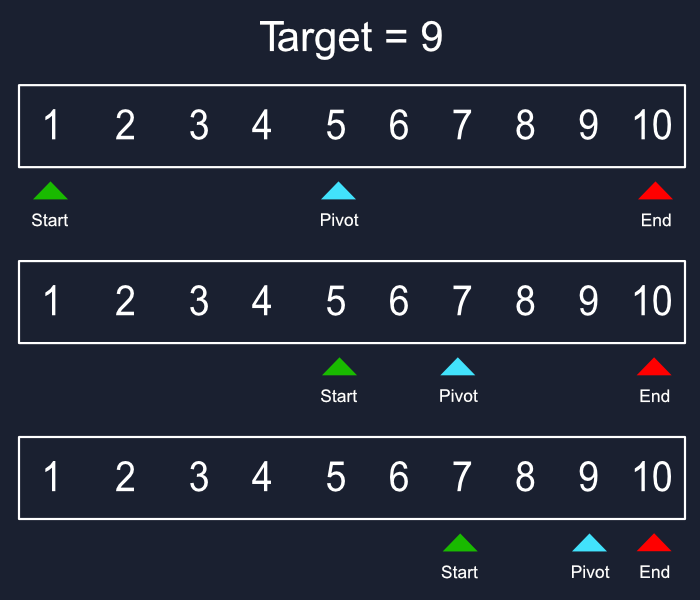
With each step we are cutting our data set in half, completely ignoring what we don’t need, giving us a time complexity of O(logn). If we ran a search for a number in an array of a million items that took ten steps, a billion item search may only take 15-20 steps.
const binary = (arr, target) => {
let start = 0;
let end = arr.length;
let pivot = Math.floor((start + end) / 2);
let steps = 0;
for (let i = 0; i < arr.length; i++) {
if (arr[pivot] !== target) {
if (target < arr[pivot]) end = pivot;
else start = pivot;
pivot = Math.floor((start + end) / 2);
steps++;
};
if (arr[pivot] === target) return `Found: ${target} in ${steps} steps`;
};
return 'Nothing Found';
};
console.log(linear(unsortedArr, 40)); // Nothing Found
console.log(binary(arr, 44)); // 5 steps in 8 Milliseconds
console.log(binary(arr, 43)); // 2 steps in 7 Milliseconds
Binary search comes with the big drawback of only allowing us to do this on sorted arrays, but there are other solutions based around pre-sorting your data before a search.
Conclusion
This is only one way of applying a binary search but the idea can be reconfigured for various data structures, as long as it’s sorted. In the future, I hope we can explore using this technique for traversing more advanced datasets at lightning fast speeds ⚡.
Thanks for learning with the DigitalOcean Community. Check out our offerings for compute, storage, networking, and managed databases.
This textbox defaults to using Markdown to format your answer.
You can type !ref in this text area to quickly search our full set of tutorials, documentation & marketplace offerings and insert the link!

Get our biweekly newsletter
Sign up for Infrastructure as a Newsletter.

Hollie's Hub for Good
Working on improving health and education, reducing inequality, and spurring economic growth? We'd like to help.

Become a contributor
Get paid to write technical tutorials and select a tech-focused charity to receive a matching donation.

